基于MATLAB的牛头刨床主切削机构运动仿真

吴广益，于光忠

(德州职业技术学院，山东 德州 253034)

牛头刨床是机械制造企业常用的金属加工机床之一，主要用于平面和沟槽加工，其主切削运动机构由摆动导杆机构和导杆滑块机构组成，各构件运动过程中的位置、速度和加速度对刀具切削工件时的加工效率和平稳性有着非常大的影响。本文采用矢量法构建机构独立位置方程并对其进行分析，借助MATLAB软件计算出滑块的线位移和各杆件的角位移，并最终得到牛头刨床主运动机构的动画，解决了利用力学分析和手工绘图精度差、效率慢、不容易理解的问题。

牛头刨床主切削运动机构的运动简图如图1所示。

图1 牛头刨床主切削运动机构运动简图

该机构的输入运动为构件1以角速度ω1作匀速转动，输出运动有滑块2的平面运动、导杆3的摆动、连杆4的平面运动和杆件5的移动。为了对该机构进行运动分析，需要在图1所示的直角坐标系中将各构件表示为杆矢，并将每个矢量向x和y轴方向做投影得出运动方程[1,2]。

首先由杆矢CA(杆长为l6)、杆矢AB(杆长为l1)和杆矢CB(杆长为s3)画出如图2所示的封闭矢量三角形，列出其矢量方程：

l6+l1=s3.

(1)

将式(1)向x和y轴作投影可得：

(2)

解方程得：

(3)

图2 CABC矢量封闭图形

(4)

将式(4)向x和y轴作投影：

(5)

解方程得:

(6)

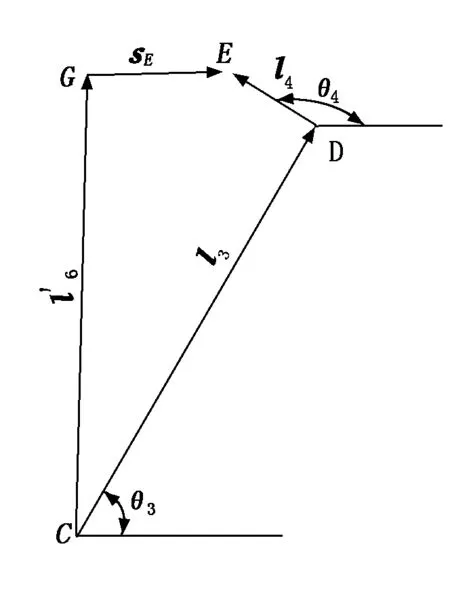
图3 CDEGC矢量封闭图形

2.1 编写主程序ntbc1.m

%1.输入已知数据

clear;

l1=0.110;

l3=0.535;

l4=0.134;

l6=0.380;

l61=0.524;

omega1=1;

hd=pi/180;

du=180/pi;

2.2 编写计算牛头刨床主切削运动机构中构件的线位移(或角位移)程序ntbc2.m(需调用子程序ntbc4.m)

%2.调用子函数ntbc4计算牛头刨床主切削运动机构的位移(或角位移)

for n1=1:459

theta1(n1)=-2*pi+5.8119+(n1-1)*hd;

ll=[l1,l3,l4,l6,l61];

[theta]=ntbc4(theta1(n1),ll);

s3(n1)=theta(1); %s3表示滑块2相对于导杆CD的线位移

theta3(n1)=theta(2);%theta3表示导杆3的角位移

theta4(n1)=theta(3);%theta4表示连杆4的角位移

sE(n1)=theta(4); %sE表示杆5的线位移

end

2.3 编写牛头刨床主切削运动机构的仿真程序ntbc3.m

%3.牛头刨床主切削运动机构仿真动画

figure(1);

m=moviein(20);

j=0;

for n1=1:5:360

j=j+1;

clf;

x(1)=0;y(1)=0;

x(2)=(s3(n1)*1000-50)*cos(theta3(n1));

y(2)=(s3(n1)*1000-50)*sin(theta3(n1));

x(3)=0;y(3)=l6*1000;

x(4)=l1*1000*cos(theta1(n1));

y(4)=s3(n1)*1000*sin(theta3(n1));

x(5)=(s3(n1)*1000+50)*cos(theta3(n1));

y(5)=(s3(n1)*1000+50)*sin(theta3(n1));

x(6)=l3*1000*cos(theta3(n1));

y(6)=l3*1000*sin(theta3(n1));

x(7)=l3*1000*cos(theta3(n1))+l4*1000*cos(theta4(n1));

y(7)=l3*1000*sin(theta3(n1))+l4*1000*sin(theta4(n1));

x(8)=l3*1000*cos(theta3(n1))+l4*1000*cos(theta4(n1))-900;

y(8)=l61*1000;

x(9)=l3*1000*cos(theta3(n1))+l4*1000*cos(theta4(n1))+600;

y(9)=l61*1000;

x(10)=(s3(n1)*1000-50)*cos(theta3(n1));

y(10)=(s3(n1)*1000-50)*sin(theta3(n1));

x(11)=x(10)+25*cos(pi/2-theta3(n1));

y(11)=y(10)-25*sin(pi/2-theta3(n1));

x(12)=x(11)+100*cos(theta3(n1));

y(12)=y(11)+100*sin(theta3(n1));

x(13)=x(12)-50*cos(pi/2-theta3(n1));

y(13)=y(12)+50*sin(pi/2-theta3(n1));

x(14)=x(10)-25*cos(pi/2-theta3(n1));

y(14)=y(10)+25*sin(pi/2-theta3(n1));

x(15)=x(10);

y(15)=y(10);

x(16)=0;

y(16)=0;

x(17)=0;

y(17)=l6*1000;

k=1:2;

plot(x(k),y(k));

hold on;

k=3:4;

plot(x(k),y(k));

hold on;

k=5:9;

plot(x(k),y(k));

hold on;

k=10:15;

plot(x(k),y(k));

hold on;

k=16:17;

plot(x(k),y(k));

hold on;

grid on;

axis ([-500 600 0 650]);

title("牛头刨床主切削运动机构");

grid on;

xlabel("mm");

ylabel("mm");

plot(x(1),y(1),"o");

plot(x(3),y(3),"o");

plot(x(4),y(4),"o");

plot(x(6),y(6),"o");

plot(x(7),y(7),"o");

hold on;

grid on;

xlabel("mm");

ylabel("mm");

axis([-400 600 0 650]);

m(j)=getframe;

end;

movie(m);

2.4 编写子程序ntbc4.m

function[theta]=ntbc4(theta1,ll)[4]

l1=ll(1);

l3=ll(2);

l4=ll(3);

l6=ll(4);

l61=ll(5);

%4.计算线位移和角位移

s3=sqrt((l1*cos(theta1))*(l1*cos(theta1))+(l6+l1*sin(theta1))*(l6+l1*sin(theta1)));

theta3=acos((l1*cos(theta1))/s3);

theta4=pi-asin((l61-l3*sin(theta3))/l4);

sE=l3*cos(theta3)+l4*cos(theta4);

theta(1)=s3;

theta(2)=theta3;

theta(3)=theta4;

theta(4)=sE;

end

将编写的各部分MATLAB程序录入到MATLAB R2016b应用程序中，编译通过后执行文件，最终得到牛头刨床主切削运动机构的仿真动画，仿真动画结束后的图形如图4所示。

图4 牛头刨床主切削运动机构图形

本文根据牛头刨床主切削运动机构的运动简图，运用矢量解析法建立运动方程，并求解出滑块2、构件5的线位移和导杆3、连杆4的角位移，结合MATLAB编程对其进行运动仿真，形象直观地展现出各构件的运动过程，为牛头刨床主切削运动机构的创新设计和运动分析奠定了基础。

猜你喜欢导杆角位移滑块一种塑料型材热刀的自动张紧装置橡塑技术与装备(2022年7期)2022-07-06心形曲柄导杆间歇机构分析与综合机械设计与制造工程(2022年1期)2022-02-19一种压电驱动的角位移微动平台设计与优化机电信息(2021年17期)2021-07-01发动机扭转减振皮带轮的匹配试验研究内燃机与配件(2020年22期)2020-09-10Cr12MoV导杆热处理开裂分析模具制造(2019年10期)2020-01-06基于离散小波变换方法的信号去噪应用研究课程教育研究·学法教法研究(2018年14期)2018-08-11λ对曲柄摆动导杆机构的运动特性影响华北理工大学学报(自然科学版)(2017年4期)2017-11-29门把手消毒滑块婚姻与家庭·性情读本(2017年1期)2017-02-16C空间中肢体参数的测量方法光学仪器(2016年5期)2017-01-12前模滑块注射模设计中国塑料(2015年9期)2015-10-14