徐 港,王 晨,谭激扬
(湘潭大学 数学与计算科学学院,湖南 湘潭 411105)
在风险理论中,精确解通常都是在模型中各参数已知的情况下获得的.但在现实中,索赔量的分布往往是部分或者完全未知的,我们仅能通过分析历史数据(样本数据),在一定误差范围内得出近似解.直接从非参数估计思想出发可以很好地解决数据分布未知带来的问题.比如Mnatsakanov[1]就在给定索赔样本的情况下,运用拉普拉斯变换估计出了索赔密度未知时的破产概率.Qin[2]在初始资本为零且索赔分布未知的经典风险模型中,考虑在给定索赔样本的情况下,讨论有限时间生存概率的一致估计问题.更多非参数方法在保险模型中的应用研究参考文献[3-4].随着学者们的不断深入探索和研究,非参数方法逐渐成为风险理论领域的一种重要方法.借助计算机的算力,非参数估计的良好性质得以展现,估计的精度可以随着样本量的增加而提高,例如文献[5]表明当样本量相当大时,经验分布函数是总体分布函数的一个良好近似.核密度估计是一种十分常用的非参数估计方法,许多学者对其进行了探讨研究.例如,郭生练等[6]将核估计应用在洪水的推求设计中,通过实测资料分析得出非参数模型具有优良的拟合能力.刘海燕等[7]讨论了密度函数的核估计方法,并且得到了估计量的逐点相合性.谭英平[8]把核密度估计运用在个体损失分布的估计上.
自从De Finetti提出最优红利问题以来,众多学者研究了各种风险模型中的最优分红问题,其中包括许多对常红利边界下复合泊松风险模型的红利问题的研究.文献[9]在延迟索赔风险模型中讨论了最优红利问题,并利用随机样本点构造出一个随机算子,从而获得最优红利策略的估计量.受此启发,本文将非参数估计方法应用到了随机算子的构造上,以此求得相关问题的近似解.
除此之外,扩散近似也是风险理论中一个十分经典的近似方法.Iglehart于1969年在精算工作中引入扩散近似方法,随后被许多学者用来研究盈余过程的破产概率和红利策略等问题,例如文献[10-14].受此启发,本文构建出相应的扩散近似模型对红利期望现值进行估计.
在精算领域扩散近似方法和近期出现的随机算子方法具有很好的应用价值,但还未有文献对这两种方法近似效果进行对比研究.因此,本文考虑复合泊松风险模型,在红利边界策略下,结合非参数估计思想提出两种随机算子近似方法,并与扩散近似方法作数值计算对比,从期望红利现值和最优红利边界两方面来探讨几种方法的近似效果.
考虑复合泊松风险模型,t时刻的盈余描述如下
(1)

(2)
本文称模型(2)为扩散近似模型,其中,B(t)是一个标准布朗运动.
本文中,对复合泊松风险模型作一修正,引入一个常数边界策略b(b≥0). 设定在时刻t(t=0,1,2,…)周期性地进行红利分配,即在这样的时刻若盈余超过b,则将超过b的部分作为红利分配给股东,反之则不分红.假设仅在这些整数时刻观察盈余过程是否破产,并根据情况作红利决策.以D(u,b)表示破产前红利现值总和(贴现因子为0 V(u,b)=E[D(u,b)|U(0)=u]. 本文中总是假设0≤u≤b. 在不发生混淆时,也用V(u)表示V(u,b). 对于复合泊松风险模型,由于它的索赔时间间隔服从指数分布,且指数分布具有无记忆性,于是可知盈余过程U(t)具有独立增量性.据此对破产前所支付红利的期望现值进行求解.以时刻t=1为更新时间点考虑各种可能的情形,根据模型(1)可得红利现值满足的方程 D(u,b)=0×I(U(1)<0)+vD(u+c-L(1),b)I(0≤U(1)≤b)+ v[D(b,b)+(u+c-L(1)-b)]I(U(1)>b). (3) (4) (5) (6) 其中Φ(x)为标准正态分布函数. 为了得到期望红利现值的估计方法,本节利用索赔量分布的估计量构造随机算子.设Xi(i=1,2,…,n)是单位时间内索赔量的独立样本点,n是样本容量.定义L∞为[0,b]上的所有有界实函数的集合.显然V(u)∈L∞.对任意A(u),B(u)∈L∞,定义L∞上的距离 显然,(L∞,d)是一个完备度量空间. (7) 在本文的实例计算中,选用高斯核函数和三角核函数: (8) (9) 定义3.1.4对任意的W(u)∈L∞,定义L∞上的两个(非随机)算子T,T0分别为 (10) (11) 定理3.1.1对任意的W(u)∈L∞,有 (12) 证明令索赔量的样本点Xi按从小到大的顺序排列并记成X(1)≤X(2)≤…≤X(n). 另外,再定义X(0)=0∧(u+c-b),X(n+1)=(u+c)∨X(n). 则存在k,k′∈{0,1,2,…,n}使得X(k)≤u+c-b≤X(k+1),X(k′) 根据定义3.1.1,当k>0时有 证明参考文献[9]和[15]的方法. 注:由定理3.2.1知,期望红利现值V(u)是算子T的唯一不动点; (2)证明方差趋于0. 由于W(u)非负,容易证得式(15)中方括号内两项的协方差小于0,因此有 Var[W(u+c-Xi)I(u+c-b (13) 因为取值于有限区间上的随机变量的方差一定有界,故可设式(13)右边两个方差的上确界分别为C1和C2,于是有 注:由定理3.2.2可知,对于期望红利现值V(u),有 =TW, (n→∞). (2)证明其方差趋于0. 其中, (14) 式(14)中i=j时的所有项之和为 另外,使用类似的方法可以得到,(14)式中i≠j时的所有项之和为 →p(x)p(y),(n→∞). 证明采用[10]中的证明方法并结合定理3.2.2和3.2.3可得结论. 注意,尽管离散型的L(1)并不存在密度函数p(x),但是仍然能够用核密度估计去拟合其分布. 例1:单位时间内索赔次数服从强度为λ=4的泊松分布,索赔金额服从参数为0.35的几何分布. 表1 例1中期望红利现值近似值对比(λ=4) 例2:单位时间内索赔次数分别服从强度为λ=3, 8, 15的泊松分布,索赔金额服从参数为0.3的几何分布.考虑不同索赔频率对近似效果的影响,其中样本量n=5 000. 表2 例2中期望红利现值近似值对比 λ=8 表2(续)λ=15 取样本量n=5 000,探究索赔频率变化对各方法关于最优红利边界近似效果的影响,其中单位时间内收取的保费仍然按c=(1+0.1)λμ1计算.固定初始盈余u=0,在不同的边界b下计算其期望红利现值.称使期望红利现值达到最大的边界为最优边界. 例3:单位时间内索赔次数分别服从强度λ=3,10的泊松分布,索赔金额服从参数为0.4的几何分布. 表3 例3中不同方法下的最优边界 表3给出了使用不同方法所获得的最优红利边界b. 通过对表中各估计值与精确值进行对比不难发现有如下规律:在索赔频率较小时,随机算子方法的近似效果更好;


3.1 随机算子的构造

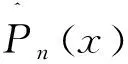
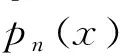





3.2 随机算子的性质

T0的唯一不动点可以看作V(u)的扩散近似值.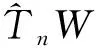

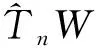




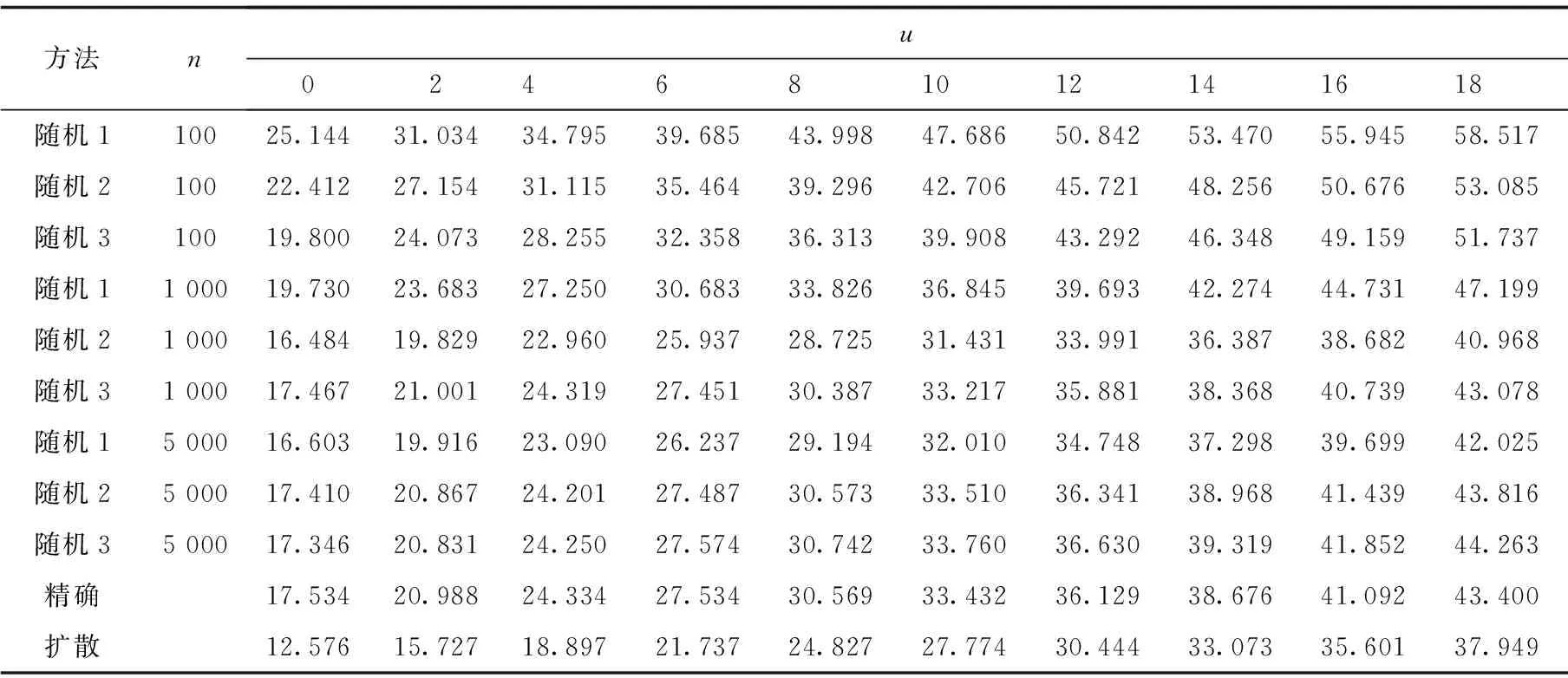
4.1 期望红利现值近似效果对比






4.2 最优边界近似效果对比
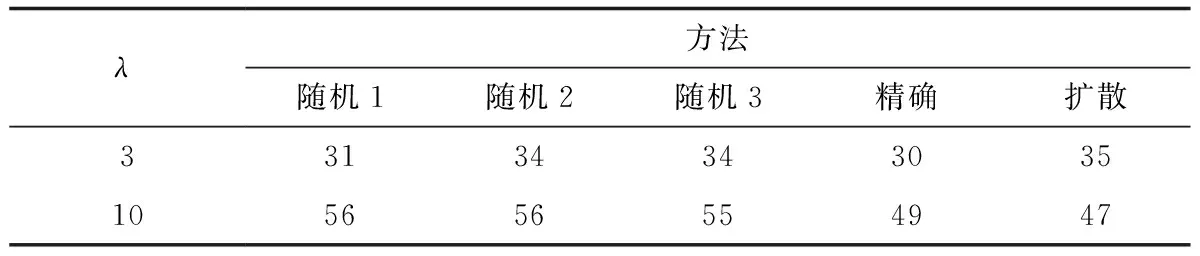
当索赔频率较大时,随机算子方法的近似效果失去优势,扩散近似方法的近似效果更好.
扩展阅读文章
推荐阅读文章
老骥秘书网 https://www.round-online.com
Copyright © 2002-2018 . 老骥秘书网 版权所有